Just like it’s been approved for the past year.

Hahaha I didn’t even think to check that. Wild

If a neoliberal party can’t win 2 out of 3 elections against a fascist, maybe they should pivot away from neoliberalism.

Right, “did Biden drop out” had a spike as seen in the first picture below. It’s hard to tell magnitude. When comparing to another phrase, it’s easy to see that the spike wasn’t even close to the spike for another election day phrase: ‘who is Kamala?’

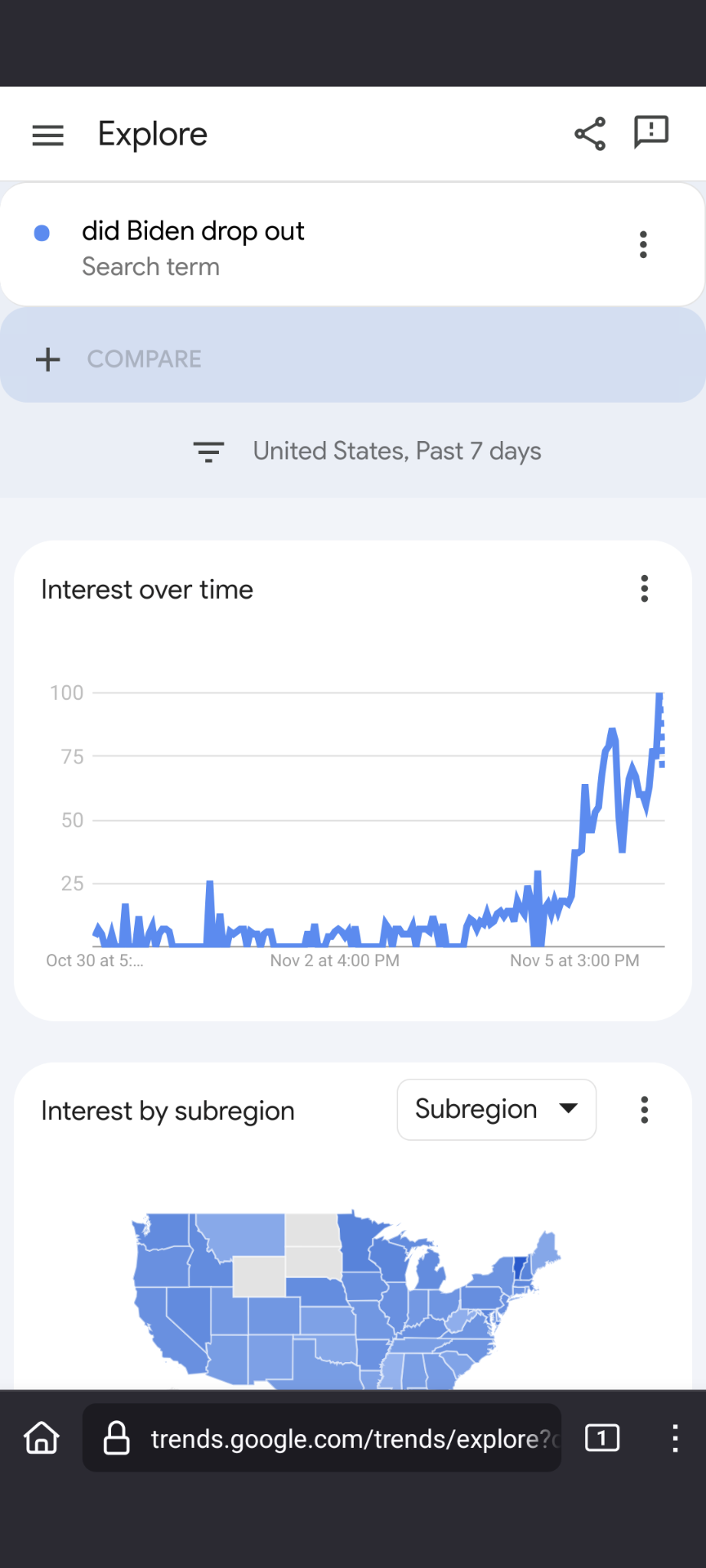
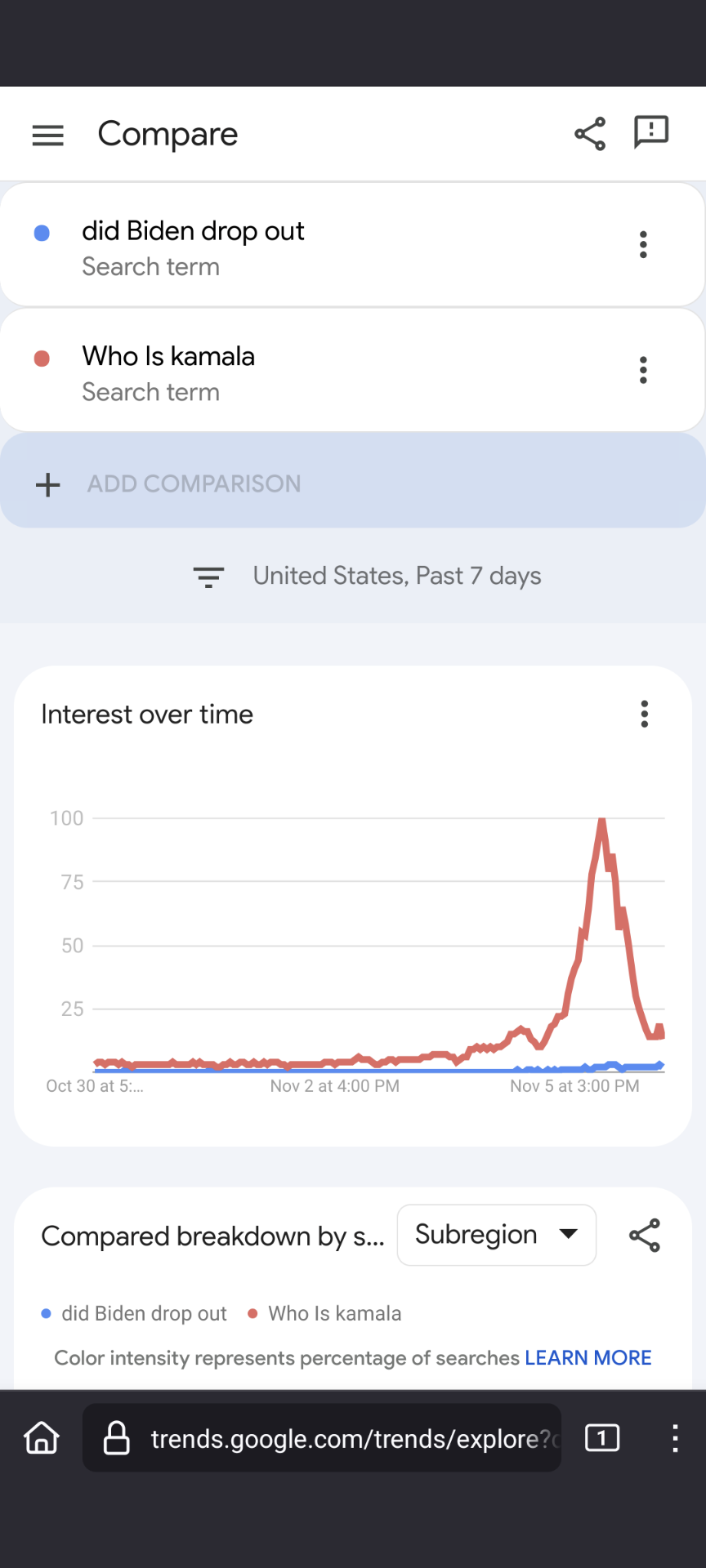
deleted by creator

Have you thought of trying to pick up another language? Started learning Spanish 4 years ago and now I can go on vacation and have conversations with locals. Also, I’m more interested in their local history because I can read it/listen to it in Spanish and practice the language at the same time.

Oh my God, I read that as “Kissinger” and thought for a terrible moment that he was still alive.

Thank you! I should’ve linked to it. The actual text does a much better job of answering OP than my attempt to summarize it.

Especially in the US, where both parties are globally “right” in both political and financial aspects, a lot of time claiming to be a centrist means that you like capitalism and bombing other countries but you support LGBT causes and are pro-choice. I think, online and especially on lemmy, that the vocal left-wing voices (correctly) see this still as aiding the right but being too cowardly to admit it.

This also ties back to the MLK quote about the ‘white centrist’ being the biggest obstacle to his movement, because they may say the right things and appear to be helpful but take no action for the movement. By staying centrist and trying to meet in the middle, would lend credibility to the voices on the other side.

Either him or Seinfeld? Feels like the stand-up bit at the beginning of one of the early episodes.

The original draft probably said “nearly a 300% increase” and then the editor didn’t know the difference between percent increase and basic multiplication.

Right, isn’t that the point of the question? What old time things did we do for one reason (cloven hooves) that turned out to be right for completely different reasons (health and safety)

In the original the possibilities for a prize behind the doors 1,2,3 are:

A) YNN B) NYN C) NNY

In (A) - A.1 you choose door 1 and then stay, you win A.2 you choose door 1 and switch, you lose A.3 you choose door 2 and stay, you lose A.4 You choose door 2 and switch, you win A.5 you choose door 3 and stay, you lose A.6 you choose door 3 and switch, you win

By staying, you lose in 2 of 3 cases (A.3 and A.5)

By switching you only lose in 1 case (A.2)

It works out for (B) and © the same way. You have a 2/3rds chance of winning if you switch and a 1/3rd chance of winning if you don’t.

This isn’t a trick or anything, the math is pretty clear and you can actually write out all the scenarios and count it up yourself. It’s just a little counterintuitive because we aren’t used to thinking in terms of conditional probabilities this way.

Another way to think about it is the probability of losing. If the contestant loses, it means that they picked correctly on their first choice and then swapped. This will happen 1/3rd of the games, because there is a 1 in 3 chance of picking correctly the first time. So, if you have a 1/3rd chance of losing by swapping, then it follows that you have a 2/3rds chance of winning by swapping (choosing incorrectly at the start and then switching to the correct door)

Do you know the third door is never correct? Because then the probability doesn’t change.

Scenario 1: You chose 1/2 at first with a 50% chance of being correct, I introduce a 3rd door (but it isn’t a legit possibility), so the actual choice for you is still 50/50 (between doors 1 and 2)

Scenario 2: If you think it’s possible that 3 could be correct (but it actually never is) then, no, you wouldn’t want to switch. By staying with your first choice has a 50% chance of winning, by switching it only has a 33% chance. But there’s no way to know this ahead of time (because as soon as you know you shouldn’t switch bc 3 is the wrong door, then you’re back in scenario 1)

Scenario 3: For completeness, let’s say the 3rd door can be correct sometimes. Then it doesn’t matter if you switch or not. It’s a 33% chance of winning either way. If there is a chance it can be correct, then your first choice doesn’t matter at all and the second choice is the ‘real’ choice bc that’s the only time you’re able to choose from all real possibilities.

The only reason that the Monty Hall problem changes probability in the second choice is because you are provided more information before the switch (that the opened door is absolutely not the one with the prize)

Agreed. And I’ve never read anything quite like The Savage Detectives. His short stories are great too, and you can find a lot of them online published by the New Yorker.

Yes, it’s the same concept. The same math/logic behind it doesn’t change. You’re choosing 1/3 or you are choosing 2/3 and I’ll tell you which of the two is incorrect. It’s just easier to visualize with 100 doors instead.

I’m not sure I’m following the other angle…there are 3 correct possibilities at the start but I can only choose 2? Or there are 2 possibilities and then you introduce a 3rd door that is never correct?

Roberto Bolaño

Because when you first picked 27, it was 1 out of 100 choices. Then I tell you that you either got it right, or it’s this other number. None of the others are correct, only 27 or 44.

So you think your 1/100 choice was better than the one I’m giving you now? On average, you’ll be right 1% of the time if you don’t switch. If you do switch, you’ll be correct 99% of the time.

Another way to think of it is: you choose 27 or you choose ALL of the other 99 numbers knowing that I’ll tell you that 98 of them are wrong and you’ll be left with the correct one out of that batch. One of those clearly has better odds, no?

Correct, extend it to 10 or 100 choices instead of 3 and it’s easy to see.

Me: Pick a number between 1 and 100.

Them: 27

Me: Okay, the number is either 27 or 44, do you want to change your choice?

Them, somehow: No, changing my choice now still has the same probability of being right as when I made my first choice.

It’s obvious that they should want to change every time.

Haha correct. I always get confused on how they’re all related too.

I also think that Taylor and Madison were second cousins or something.